Többváltozós analízis

Tartalomjegyzék

Általános tudnivalók
Jelölések
Definíciók
Tételek, állítások
Előadások \ 5.1. 1. Előadás 5.2. 2. Előadás 5.3. 3. Előadás 5.4. 4. Előadás 5.5. 5. Előadás 5.6. 6. Előadás 5.7. 7. Előadás

Általános tudnivalók

Jelölések

$ℝ^{p}$ - $p$ dimenziós valós tér
$A^{C}$ - $A$ halmaz komplementere
$ext A$ - $A$ halmaz külső pontjainak halmaza
$int A$ - $A$ halmaz belső pontjainak halmaza
$\partial A$ - $A$ halmaz határpontjainak halmaza
$\bar{A}$ - $A$ halmaz lezártja
$graph f$ - $f$ grafikonja
$γ_{c}$ - $f$ függvény $c$ -hez tartozó szintvonala
$Γ_{c}$ - $f$ függvény $c$ -hez tartozó kontúrvonala
$| \underset{―}{x} |$ - $\underset{―}{x}$ hossza
$d (\underset{―}{x}, \underset{―}{y}) = | \underset{―}{x} - \underset{―}{y} |$ - $\underset{―}{x}$ és $\underset{―}{y}$ távolsága
$grad f = \underset{―}{\nabla} f$ - $f$ függvény gradiens vektora
$f_{x}^{'}$ függvény $x$ szerinti parciális deriváltja
$f^{'}$ - függvény totális deriváltja

Definíciók

Tételek, állítások

[+ random allitasok kellenek, amiket felirtunk?]
Bolzano-Weierstrass tétel

Előadások

1. előadás

Félév tematikája

Többváltozós függvények: $f : ℝ^{p} \to ℝ$

Térgörbék: $f : ℝ \to ℝ^{p}$

Felületek: $f : ℝ^{2} \to ℝ^{p}$

Vektormezők: $f : ℝ^{p} \to ℝ^{q}$

Függvénysorozatok/sorok, hatványsorok, Fourier-sorok

Komplex függvénytani bevezető

$ℝ^{p}$ tér topológiája

Jelölés: $\underset{―}{x} \in ℝ^{p}$

Def.: * Pont környezete * Belső pontok * Külső pontok * Határpontok * Nyílt halmaz * Zárt halmaz * Halmaz lezártja

Áll.: * $int A \subseteq A \subseteq \bar{A}$ * $ext A$ mindig nyílt * $\partial A$ mindig zárt * $int A$ , $ext A$ , $\partial A$ páronként diszjunkt halmazok * $int A \cup ext A \cup \partial A = ℝ^{p}$ , ha $A \subseteq ℝ^{p}$

Példa: $A = [0; 1) esetén$ * $int A = (0; 1)$ * $ext A = (- \infty; 0) \cup (1; \infty)$ * $\partial A = {0; 1}$ * $\bar{A} = [0; 1]$

Példa: $A = {(x, y) \in ℝ^{2} : 0 < x^{2} + y^{2} < 1}$ esetén * $int A = A$ * $ext A = {x^{2} + y^{2} > 1}$ * $\partial A = {x^{2} + y^{2} = 1} \cup {(0, 0)}$

Def.: * Izolált pont * Torlódási pont

Példa: $A = {\frac{1}{n} : n \in ℕ^{p}}$ -nak $0$ -ban van torlódási pontja

Példa: $A = (0; 1]$ -nak a torlódási pontjai $[0; 1]$

Áll.: * Véges sok nyílt halmaz metszete nyílt * Akárhány nyílt halmaz uniója nyílt * Véges sok zárt halmaz uniója zárt * Akárhány zárt halmaz metszete zárt

Def.: * Összefüggő halmaz * Tartomány * Korlátos halmaz

Példa: * $(1; 3]$ összefüggő * $A = (0; 1) \cup (1; 3]$ nem összefüggő, hiszen $B = (0; 1), C = (1; 4)$

Def.: * Sorozat határértéke * Konvergens sorozat

Áll.: $lim {\underset{―}{x}}_{n} = A \Leftrightarrow \forall i < p : ({\underset{―}{x}}_{n})_{i} \to A_{i}$

Példa:

{lim}_{n \to \infty} (\frac{n - 1}{n}, {(1 + \frac{1}{n})}^{n}) = (1, e)

Áll.: * Bolzano-Weierstrass tétel: $\forall$ korlátos sorozatnak $\exists$ konvergens részsorozata * $ℝ^{p}$ -ben is igaz, hogy $\forall$ Cauchy sorozat konvergens

Kétváltozós függvények

Def.: * Grafikon * Kontúrvonal * Szintvonal

Példa: $f (x, y) = \sqrt{x^{2} + y^{2}} = z$ , Mi lehet ez?

Medoldás: * Szintvonalak: $\sqrt{x^{2} + y^{2}} = c$ - minden szintvonal kör * Síkmetszés $[x, z]$ síkkal, (ekkor $y = 0$ ): $\sqrt{x^{2}} = | x | = z$ * Tehát minden vízszintes szintvonal kör, és az egyik függőleges egy abszolútérték, így ez egy forgáskúp lesz.

2. előadás

Példa: ${lim}_{(x, y) \to (0, 0)} \frac{2 x y}{x^{2} + y^{2}} = {lim}_{(x, y) \to (0, 0)} f (x, y)$

Def.: * Két út módszer * Parciális derivált * Young tétel * Iránymenti derivált * Totális derivált * Érintősík * Gradiens vektor

Áll.: * $f_{c \underset{―}{v}}^{'} = f_{\underset{―}{v}}^{'}$ , ha $c > 0$ * $f_{- v}^{'} ({\underset{―}{x}}_{0}) = - f_{v}^{'} ({\underset{―}{x}}_{0})$ * $f$ totálisan diffható $x_{0}$ pontban és $f^{'} ({\underset{―}{x}}_{0}) = \underset{―}{A} \Leftrightarrow {lim}_{\underset{―}{x} \to {\underset{―}{x}}_{0}} \frac{f (\underset{―}{x}) - f ({\underset{―}{x}}_{0}) - \underset{―}{A} (\underset{―}{x} - {\underset{―}{x}}_{0})}{| \underset{―}{x} - {\underset{―}{x}}_{0} |} = 0$

Áll.: Tegyük fel, hogy $f$ totálisan diffható ${\underset{―}{x}}_{0}$ pontban $f : ℝ^{p} \to ℝ$ . Ekkor: 1. $f$ folytonos ${\underset{―}{x}}_{0}$ -ban 2. $f$ iránymenti deriváltjai léteznek az ${\underset{―}{x}}_{0}$ -ban és $f_{\underset{―}{v}}^{'} ({\underset{―}{x}}_{0}) = \underset{―}{f^{'}} ({\underset{―}{x}}_{0}) \cdot \frac{\underset{―}{v}}{| \underset{―}{v} |} = \underset{―}{\nabla} f ({\underset{―}{x}}_{0}) \frac{\underset{―}{v}}{| \underset{―}{v} |}$ 3. $\underset{―}{f^{'}} ({\underset{―}{x}}_{0}) = \underset{―}{\nabla} f (x_{0})$ totálisan diffható $f \Rightarrow f$ parciális deriváltjai is léteznek.

Bizonyítások.: 1. A totális derivált definíciója szerint a folytonosság így teljesül:

{lim}_{\underset{―}{x} \to {\underset{―}{x}}_{0}} f (\underset{―}{x}) = {lim}_{\underset{―}{x} \to {\underset{―}{x}}_{0}} f ({\underset{―}{x}}_{0}) + {lim}_{\underset{―}{x} \to {\underset{―}{x}}_{0}} \underset{―}{A} \cdot (\underset{―}{x} - {\underset{―}{x}}_{0}) + {lim}_{\underset{―}{x} \to {\underset{―}{x}}_{0}} ε (\underset{―}{x}) | \underset{―}{x} - {\underset{―}{x}}_{0} | \newline = f ({\underset{―}{x}}_{0}) + \underset{―}{A} \cdot \underset{―}{0} + 0 = f ({\underset{―}{x}}_{0})

Iránymenti derivált átírható ha totálisan diffható a függvényünk:

f_{\underset{―}{v}}^{'} = {lim}_{t \to 0} \frac{f ({\underset{―}{x}}_{0} + t \frac{\underset{―}{v}}{| \underset{―}{v} |})}{t} = {lim}_{t \to 0} \frac{f ({\underset{―}{x}}_{0}) + \underset{―}{A} t \frac{\underset{―}{v}}{| \underset{―}{v} |} + ε (\underset{―}{x}) t \frac{\underset{―}{v}}{| \underset{―}{v} |} - f ({\underset{―}{x}}_{0})}{t} \newline = {lim}_{t \to 0} \underset{―}{A} \frac{\underset{―}{v}}{| \underset{―}{v} |} + ε (\underset{―}{x}) \frac{\underset{―}{v}}{| \underset{―}{v} |}

A totálisan deriválhatóság miatt $ε (\underset{―}{x}) = ε ({\underset{―}{x}}_{0} + t \frac{\underset{―}{v}}{| \underset{―}{v} |})$ , ami $0$ -ba tart.

f_{\underset{―}{v}}^{'} ({\underset{―}{x}}_{0}) = \underset{―}{A} \frac{\underset{―}{v}}{| \underset{―}{v} |} = f^{'} ({\underset{―}{x}}_{0}) \cdot \frac{\underset{―}{v}}{| \underset{―}{v} |}

A 2. pontból, illetve a totális derivált, iránymenti derivált, és parciális derivált definícióiból következik: Tekintsük az $1$ -es dimenzió irányvektorát:

\underset{―}{v} = [\begin{matrix} 1 \\ 0 \\ ⋮ \\ 0 \end{matrix}], f_{\underset{―}{v}}^{'} = \underset{―}{A} \cdot \underset{―}{v} = A_{1} = f_{x_{1}}^{'}

Tehát a parciális derivált egy speciális iránymenti derivált. Hasonlóan megismételhetjük minden $x_{1}, x_{2}, \dots, x_{p}$ -vel. Így megkapjuk $\underset{―}{A}$ minden koordinátáját:

\underset{―}{A} = (f_{x_{1}}^{'}, f_{x_{2}}^{'}, \dots, f_{x_{p}}^{'}) = \underset{―}{f^{'}} = \underset{―}{\nabla} f

3. előadás

Def.: * Totális differenciálhatóság

Megj.: Érintő hipersík egyenlete: $z = f ({\underset{―}{x}}_{0}) + f^{'} ({\underset{―}{x}}_{0}) (\underset{―}{x} - {\underset{―}{x}}_{0})$ , ez a hipersík átmegy az $({\underset{―}{x}}_{0}, f ({\underset{―}{x}}_{0})) \in ℝ^{p + 1}$ ponton $ℝ^{p + 1}$ -ben

Def.: * Folytonos differenciálhatóság

Áll.: Ha $f$ differenciálható ${\underset{―}{x}}_{0}$ akkor: * $f$ folytonos ${\underset{―}{x}}_{0}$ -ban * $f$ parciális deriváltjai $\exists$ -nek, és ${\underset{―}{f}}^{'} ({\underset{―}{x}}_{0}) =^{áll} \underset{―}{\nabla} f ({\underset{―}{x}}_{0}) =^{def} {(f_{x_{1}}^{'} ({\underset{―}{x}}_{0}), f_{x_{2}}^{'} ({\underset{―}{x}}_{0}), \dots, f_{x_{p}}^{'} ({\underset{―}{x}}_{0}))}^{T}$ * $f$ iránymenti deriváltjai $\exists$ -nek, és: $f_{\underset{―}{v}}^{'} ({\underset{―}{x}}_{0}) = \underset{―}{\nabla} f ({\underset{―}{x}}_{0}) \cdot \frac{\underset{―}{v}}{| \underset{―}{v} |}$ , ahol $\underset{―}{v} \in ℝ^{p} ⧵ {0}$

Áll.: Ha $f$ folytonosan differenciálható, akkor totálisan differenciálható.

Biz.: Tfh. $f$ folytonosan diffható $(x_{0}, y_{0})$ pontban, ekkor definícióból tudjuk, hogy a parciális deriváltak ( $f_{x}^{'}$ , $f_{y}^{'}$ ) léteznek ott.

Kell: $f$ totálisan diffható $(x_{0}, y_{0})$ -ban, azaz kell:

{lim}_{(x, y) \to (x_{0}, y_{0})} \textcolor r e d α : = {lim}_{(x, y) \to (x_{0}, y_{0})} \frac{f (x, y) - f (x_{0}, y_{0}) - f_{x}^{'} (x_{0}, y_{0}) (x - x_{0}) - f_{y}^{'} (x_{0}, y_{0}) (y - y_{0})}{\sqrt{(x - x_{0})^{2} + (y - y_{0})^{2}}} \stackrel ? = 0

Most hozzáadtunk és kivonunk $f (x_{0}, y)$ -t.

{lim}_{(x, y) \to (x_{0}, y_{0})} \frac{f (x, y) \textcolor p u r p l e - f (x_{0}, y) - f_{x}^{'} (x_{0}, y_{0}) (x - x_{0}) \textcolor p u r p l e + f (x_{0}, y) - f (x_{0}, y_{0}) - f_{y}^{'} (x_{0}, y_{0}) (y - y_{0})}{\sqrt{(x - x_{0})^{2} + (y - y_{0})^{2}}} = 0 \newline

A Lagrange-tétel-ből következik, hogy $\exists \tilde{x}$ az $x, x_{0}$ között:

f (x, y) - f (x_{0}, y) = g (x) - f (x_{0}) = g (\tilde{x}) (x - x_{0}) = f_{x}^{'} (\tilde{x}, y) (x - x_{0})

Hasonlóan működik az $f_{y}^{'}$ -al is. Visszahelyettesítve:

{lim}_{(x, y) \to (x_{0}, y_{0})} \frac{\textcolor g r e e n f_{x}^{'} (\tilde{x}, y) (x - x_{0}) - f_{x}^{'} (x_{0}, y_{0}) (x - x_{0}) \textcolor g r e e n f_{y}^{'} (x_{0}, \tilde{y}) (y - y_{0}) - f_{y}^{'} (x_{0}, y_{0}) (y - y_{0})}{\sqrt{(x - x_{0})^{2} + (y - y_{0})^{2}}} = 0

Szétbontva:

{lim}_{(x, y) \to (x_{0}, y_{0})} [f_{x}^{'} (\tilde{x}, y) - f_{x}^{'} (x_{0}, y_{0})] \frac{x - x_{0}}{\sqrt{(x - x_{0})^{2} + (y - y_{0})^{2}}} + [f_{y}^{'} (x_{0}, \tilde{y}) - f_{y}^{'} (x_{0}, y_{0})] \frac{y - y_{0}}{\sqrt{(x - x_{0})^{2} + (y - y_{0})^{2}}}

Háromszög egyenlőtlenség miatt:

{lim}_{(x, y) \to (x_{0}, y_{0})} | \frac{x - x_{0}}{\sqrt{(x - x_{0})^{2} + (y - y_{0})^{2}}} | < 1, {lim}_{(x, y) \to (x_{0}, y_{0})} | \frac{y - y_{0}}{\sqrt{(x - x_{0})^{2} + (y - y_{0})^{2}}} | < 1,

Illetve:

{lim}_{(x, y) \to (x_{0}, y_{0})} f_{x}^{'} (\tilde{x}, y) - f_{x}^{'} (x_{0}, y_{0}) = f_{x}^{'} (x_{0}, y_{0}) - f_{x}^{'} (x_{0}, y_{0}) = 0 \newline {lim}_{(x, y) \to (x_{0}, y_{0})} f_{y}^{'} (x_{0}, \tilde{y}) - f_{y}^{'} (x_{0}, y_{0}) = f_{y}^{'} (x_{0}, y_{0}) - f_{y}^{'} (x_{0}, y_{0}) = 0

Tehát:

{lim}_{(x, y) \to (x_{0}, y_{0})} | \textcolor r e d α | \leq 0 \cdot 1 + 0 \cdot 1 = 0 \newline \textcolor r e d α \to 0

Tehát ekkor $f$ totálisan diffható

Áll.: Ha $f$ kétszer folytonosan diffható akkor $f_{x y}^{″} = f_{y x}^{″}$ , ez a Young tétel.

4. Előadás

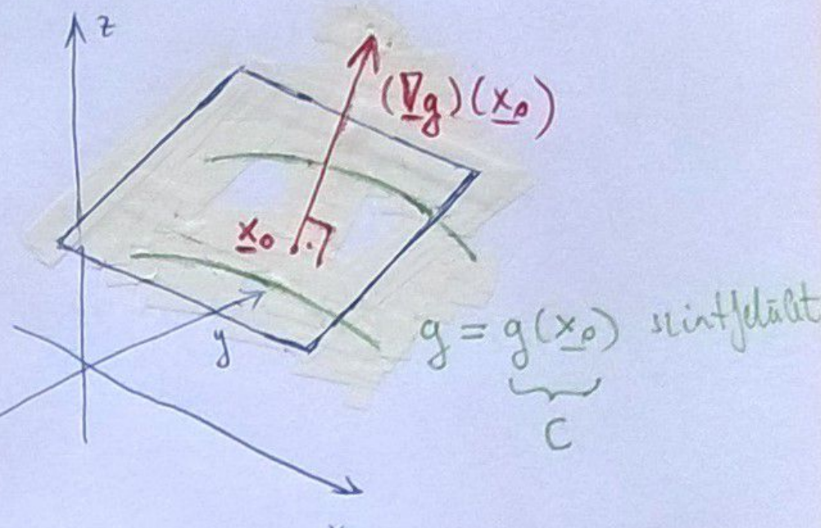
Áll.: Tegyük fel, hogy $g : ℝ^{3} \to ℝ$ totálisan diffható az ${\underset{―}{x}}_{0}$ pontban. Ekkor a $g (\underset{―}{x}) = g ({\underset{―}{x}}_{0})$ szintfelület ${\underset{―}{x}}_{0}$ pontbeli érintősíkja:

(\underset{―}{\nabla} g) ({\underset{―}{x}}_{0}) \cdot (\underset{―}{x} - {\underset{―}{x}}_{0}) = 0

Biz.: Mivel $g$ totálisan diffható az ${\underset{―}{x}}_{0}$ pontban, ezért $(\underset{―}{\nabla} g) ({\underset{―}{x}}_{0})$ merőleges az ${\underset{―}{x}}_{0}$ ponton átmenő szintfelületre, így $\underset{―}{n} = \underset{―}{\nabla} g ({\underset{―}{x}}_{0})$ az érintősíknak normálvektora.

alt text

Gradiensvektor tulajdonságai

Áll.: Tfh. $ℝ^{p} \to ℝ$ totálisan diffható ${\underset{―}{x}}_{0} \in ℝ^{p}$ pontban. Ekkor: 1. $\underset{―}{\nabla} f ({\underset{―}{x}}_{0})$ a legnagyobb növekedés iránya ${\underset{―}{x}}_{0}$ pontban 2. $- \underset{―}{\nabla} f ({\underset{―}{x}}_{0})$ a legnagyobb csökkenés iránya ${\underset{―}{x}}_{0}$ pontban 3. $| f_{\underset{―}{\nabla} f ({\underset{―}{x}}_{0})}^{'} ({\underset{―}{x}}_{0}) | = | \underset{―}{\nabla} f ({\underset{―}{x}}_{0}) |$ , $| f_{- \underset{―}{\nabla} f ({\underset{―}{x}}_{0})}^{'} ({\underset{―}{x}}_{0}) | = | \underset{―}{\nabla} f ({\underset{―}{x}}_{0}) |$ 4. $\underset{―}{\nabla} f ({\underset{―}{x}}_{0}) ⟂ f = f ({\underset{―}{x}}_{0})$ szintvonalra 5. ${max}_{\underset{―}{v}} f_{\underset{―}{v}}^{'} ({\underset{―}{x}}_{0}) = | \underset{―}{\nabla} f ({\underset{―}{x}}_{0}) |$ 6. ${min}_{\underset{―}{v}} f_{\underset{―}{v}}^{'} ({\underset{―}{x}}_{0}) = - | \underset{―}{\nabla} f ({\underset{―}{x}}_{0}) |$

Biz.: $\underset{―}{v} \in ℝ^{p}$

{\underset{―}{f^{'}}}_{\underset{―}{v}} ({\underset{―}{x}}_{0}) = \underset{―}{\nabla} f ({\underset{―}{x}}_{0}) \cdot \frac{\underset{―}{v}}{| \underset{―}{v} |} = | \underset{―}{\nabla} f ({\underset{―}{x}}_{0}) | \cdot | \frac{\underset{―}{v}}{| \underset{―}{v} |} | \cdot \cos α

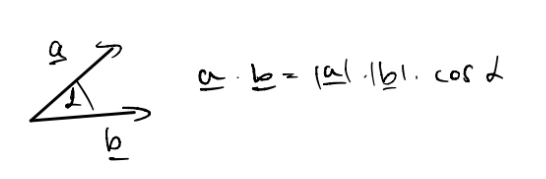
alt text

Látható, hogy akkor lesz maximális ${\underset{―}{f^{'}}}_{\underset{―}{v}} ({\underset{―}{x}}_{0})$ , ha $c o s α = 1$ , tehát $α = 0 °$ . Ezzel ekvivalens, hogy $\underset{―}{\nabla} f | | \underset{―}{v}$ és $\underset{―}{\nabla} f | | c \cdot \underset{―}{v} (c > 0)$ . Ilyenkor $| f_{\underset{―}{v}}^{'} ({\underset{―}{x}}_{0}) | = | \underset{―}{\nabla} f ({\underset{―}{x}}_{0}) |$ . (5. állítás) Minimum esetén hasonlóan eljárva, csak $α = - 1$ és $c < 0$ azt kapjuk, hogy $| f_{\underset{―}{v}}^{'} ({\underset{―}{x}}_{0}) | = - | \underset{―}{\nabla} f ({\underset{―}{x}}_{0}) |$ . (6. állítás)

Áll.: Ha $\underset{―}{\nabla} f ({\underset{―}{x}}_{0}) \neq \underset{―}{0}$ és $f$ totálisan diffható ${\underset{―}{x}}_{0}$ -ban, akkor $f = c$ , $c = f ({\underset{―}{x}}_{0})$ szintvonal ${\underset{―}{x}}_{0}$ egy kis környezetében paraméterezhető $x (t)$ , $y (t)$ diffható függvényekkel.

Áll.: Tfh. $f : ℝ^{2} \to ℝ$ , $x, y : ℝ \to ℝ$ diffhatóak. $t \in ℝ$ Ekkor $\frac{d}{d t} f (x (t), y (t)) : ℝ \to ℝ = \textcolor g r e e n {\underset{―}{f}}^{'} (x (t), y (t)) \cdot (x^{'} (t), y^{'} (t))$

\textcolor g r e e n {\underset{―}{f}}^{'} (x (t), y (t)) = (f_{x}^{'} (x (t), y (t)), f_{y}^{'} (x (t), y (t))) = \textcolor o r a n g e f_{x}^{'} |_{(x (t), y (t)) = p (t)} \cdot x^{'} (t) + f_{y}^{'} |_{(x (t), y (t)) = p (t)} \cdot y^{'} (t)

$c = f (x (t), y (t)) / \frac{d}{d t}$

0 = \textcolor o r a n g e f_{x}^{'} |_{p (t)} \cdot x^{'} (t) + f_{y}^{'} |_{p (t)} \cdot y^{'} (t) = \underset{―}{\nabla} f ({\underset{―}{x}}_{0}) \cdot (x^{'} (t_{0}), y^{'} (t_{0}))

azért teljesül, mert $\underset{―}{\nabla} f ({\underset{―}{x}}_{0})$

merőleges $(x^{'} (t_{0}), y^{'} (t_{0}))$

érintővektorra.

Áll.: Tfh.: $g : ℝ^{3} \to ℝ$ totálisan diffható ${\underset{―}{x}}_{0} \in ℝ^{3}$ pontban, és $\underset{―}{\nabla} g ({\underset{―}{x}}_{0}) \neq \underset{―}{0}$ . Ekkor a $g = c, c = g ({\underset{―}{x}}_{0})$ szintfelületnek (hasonló a szintvonalhoz szintvonal) az ${\underset{―}{x}}_{0}$ pontban van érintősíkja, és ez $\underset{―}{\nabla} g ({\underset{―}{x}}_{0}) \cdot (\underset{―}{x} - {\underset{―}{x}}_{0}) = 0$

Biz.: A gradiens vektor egyik tulajdonsága, hogy a $\underset{―}{0} \neq \underset{―}{\nabla} g ({\underset{―}{x}}_{0})$ merőleges a $g = c$ szintfelületre, így a szintfelület érintősíkjának normálvektora pontosan $\underset{―}{\nabla} g ({\underset{―}{x}}_{0})$ . Tehát a sík egyenlete: $\underset{―}{n} \cdot (\underset{―}{x} - {\underset{―}{x}}_{0}) = \underset{―}{\nabla} g ({\underset{―}{x}}_{0}) \cdot (\underset{―}{x} - {\underset{―}{x}}_{0}) = 0$ .

alt text

5. Előadás

Elmaradt

6. Előadás

Diff. egyenletek

Diffegyenlet definíciók

Példa.: Tfh $f (x, y) = - \frac{P (x, y)}{Q (x, y)}$ . Tfh. $D \subseteq ℝ^{2}$ tartományon $Q \neq 0$ . Ekkor:

y^{'} = - \frac{P (x, y)}{Q (x, y)} \newline Q y^{'} = - P \newline P + q y^{'} = 0 \newline P + Q \frac{d y}{d x} = 0

Azaz formálisan átírva:

P d x + Q d y = 0

Def.: egyszeresen összefüggő tartomány

Példa.: Adjuk meg a $(2 x y) d x + (2 y + x^{2}) d y = 0$ differenciálegyenlet általános megoldását és az $y (1) = 2$ kezdeti feltételt teljesítő megoldást.

Megoldás.: A $P (x, y) d x + Q (x, y) d y = 0$ formában $P (x, y) = 2 x y$ , $Q (x, y) = (2 y + x^{2})$

Ellenőrizzük, hogy a diffegyenlet egzakt-e. Ennek két feltétele van: 1. $P, Q$ folytonosan diffhatóak az egész $R^{2}$ -en: Ez a feltétel teljesül. 2. $P_{y}^{'} \stackrel ? = Q_{x}^{'}$

P_{y}^{'} = 2 x = Q_{x}^{'}

, tehát ez a feltétel is teljesül.

Ez azt jelenti, hogy egzakt diffegyenlettel van dolgunk.

Kell egy olyan $F$ , aminek az $x$ szerinti parciális deriváltja $P$ -vel, az $y$ szerinti $Q$ -val egyenlő.

F_{x}^{'} = P = 2 x y \Rightarrow F (x, y) = \int 2 x y d x = x^{2} y + A (y)

3 F_{y}^{'} = Q = 2 y + x^{2} & = F^{'} y = x^{2} + A^{'} y x^{2} + A^{'} (y) & = 2 y + x^{2} A (y) & = y^{2} + \tilde{c} (\tilde{c} \in ℝ)

Tehát $F (x, y) = x^{2} y + y^{2} + \tilde{c} = \tilde{\tilde{c}}$ - A diffegyenlet általános megoldása:

x^{2} y + y^{2} = c

, $c \in ℝ$

( $c = \tilde{\tilde{c}} - \tilde{c}$

) - $y (1) = 2$ kezdeti feltételt teljesítő megoldás:

x = 1, y = 2

rajta van a megfelelő szintvonalon $\Rightarrow$

1^{2} \cdot 2 + 2^{2} = 6 = c

A megoldás: $x^{2} y + y^{2} = 6$

Mi van, ha a diffegyenlet nem egzakt?

Def.: - első differenciál - teljes differenciál

Áll.: Tfh. $P, Q : ℝ^{2} \to ℝ$ folytonosan diffható egy $D \subseteq ℝ^{2}$ egyszeresen összefüggő tartományban, azaz $f_{x}^{'} = P$ és $f_{y}^{'} = Q$ Ekkor $P d x + Q d y$ teljes differenciál $\Leftrightarrow$ $P_{y}^{'} = Q_{x}^{'}$ .

7. Előadás

$ℝ^{n} \to ℝ^{m}$ függvények differenciálása

Def.: - lineáris leképezés - többdimenziós diffhatóság

Emlékeztető:

f : ℝ^{n} \to ℝ

, ha $f$

diffható, akkor ${\underset{―}{f}}^{'} = \underset{―}{\nabla} f (\underset{―}{a}) = (f_{x_{1}}^{'}, f_{x_{2}}^{'}, \dots, f_{x_{n}}^{'}) (\underset{―}{a})$

, azaz a derivált megegyezeik a gradiensével.

Áll.:

\underset{―}{f} : ℝ^{n} \to ℝ^{m}

\underset{―}{f} = (\begin{matrix} f_{1} \\ ⋮ \\ f_{m} \end{matrix})

f

diffható $\underset{―}{a}$

-ban $\Leftrightarrow$

f_{1}, \dots, f_{m} : ℝ^{n} \to ℝ

diffható(másik definícióra visz ez a link) $\underset{―}{a}$

-ban és

3 {\underset{―}{f}}^{'} |_{\underset{―}{a}} & = {(\begin{matrix} f_{1}^{'} \\ ⋮ \\ f_{m}^{'} \end{matrix}) |}_{\underset{―}{a}} & = {(\begin{matrix} \underset{―}{\nabla} f_{1} \\ ⋮ \\ \underset{―}{\nabla} f_{m} \end{matrix}) |}_{\underset{―}{a}} & = {(\begin{matrix} \underset{―}{\nabla} f_{1} \\ ⋮ \\ \underset{―}{\nabla} f_{m} \end{matrix}) |}_{\underset{―}{a}} & = {(\begin{matrix} \frac{\partial f_{1}}{\partial x_{1}} & \dots & \frac{\partial f_{1}}{\partial x_{n}} \\ ⋮ & ⋱ & ⋮ \\ \frac{\partial f_{m}}{\partial x_{1}} & \dots & \frac{\partial f_{m}}{\partial x_{n}} \end{matrix}) |}_{\underset{―}{a}}

Áll.: (Összetett függvény deriválási szabálya) Tfh. $g : ℝ^{n} \to ℝ^{m}$ $f : ℝ^{m} \to ℝ^{e}$ . $g$ diffható $\underset{―}{a} \in ℝ^{n}$ pontban, $f$ diffható $g (\underset{―}{a}) \in ℝ^{m}$ pontban. Ekkor $f \circ g : ℝ^{n} \to ℝ^{e}$ is diffható $\underset{―}{a} \in ℝ^{n}$ -ben és

(f \circ g)^{'} (\underset{―}{a}) = \underset{―}{\underset{―}{f^{'}}} (\underset{―}{g} (\underset{―}{a})) \circ \underset{―}{\underset{―}{g^{'}}} (\underset{―}{a})

Alkalmazás.: Láncszabály különböző alakjai 1. $f : ℝ^{2} \to ℝ$ diffható, $g : ℝ \to ℝ^{2}$ diffható, tehát $f \circ g$ is diffható és

3 (f \circ g)^{'} (t) & = {\underset{―}{f}}^{'} (\underset{―}{g} (t)) \cdot {\underset{―}{g}}^{'} (t) & = {(f_{x}^{'}, f_{y}^{'}) |}_{(x (t), y (t))} & = f_{x}^{'} (x (t), y (t)) \cdot x^{'} (t) + f_{y}^{'} (x (t), y (t)) \cdot y^{'} (t)

Többváltozós analízis

Tartalomjegyzék

Általános tudnivalók

Jelölések

Definíciók

Tételek, állítások

Előadások

1. előadás

Félév tematikája

ℝp tér topológiája

Kétváltozós függvények

2. előadás

3. előadás

4. Előadás

Gradiensvektor tulajdonságai

5. Előadás

6. Előadás

Diff. egyenletek

7. Előadás

ℝn→ℝm függvények differenciálása

$ℝ^{p}$ tér topológiája

$ℝ^{n} \to ℝ^{m}$ függvények differenciálása